The major difference between a thing that might go wrong and a thing that cannot possibly go wrong is that when a thing that cannot possibly go wrong goes wrong it usually turns out to be impossible to get at or repair.

– Douglas Adams

The symptom: Real estate investments look like a sure thing.

The example: You listen to a sales presentation for a new resort flat development in another city. The salesperson assures the audience that these properties are so valuable that the developer will buy the unit back at any time for the next ten years for the purchase price. The loan terms are also attractive at 5% for 30 years and nothing down. The more you consider the offer, the more you feel this is a sure thing. What could possibly go wrong? Since you do not put anything down, and you can always get back at least what you paid, it seems like there is no downside and substantial upside if the flat appreciates. You do not have a lot of money right now, but that is not a problem since you do not have to put anything down. You decide to purchase the flat as an investment and pay as long as you can, at which point you will either break even selling it back to the developer, or hopefully turn a profit selling it to someone else at a higher price.

It is been a few years since people stopped believing that real estate always went straight up, but we think most of us (us included) still believe that if you hold a piece of property long enough, you are likely to eventually break even. While this is not an unreasonable assumption, it is easy to build a lot of unreasonable ideas on top of it.

You will notice that we set up the above example to guarantee you will break even on the real estate transaction itself. And for this article, we are also going to (unrealistically) assume there are absolutely no sales costs, property taxes, or maintenance costs with the property. That way we can focus on only one thing: the financial leverage.

With a guarantee on the sale price and no carrying costs involved, it is easy to imagine that nothing can go wrong. As the example incorrectly assumed, “there is no downside and substantial upside”, and since there are also no upfront costs, why not take a chance?

We are sure a lot of people intuitively “smell a rat” here, but might have trouble articulating the problem. The person in the example has little money, but does not have to put anything down. At some point, he or she might not be able to continue to make the payments, but at that point the property can be automatically sold back to the developer. This is not the person’s primary residence, so it not a lifestyle problem if the property has to be sold, and the developer guarantees to pay the purchase price. It does not appear like a loss is possible. It is easy to be lured in.

Examining the Loan Schedule 

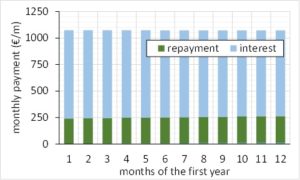
To make it completely clear what is happening, let us look at the payment schedule for the first 10 years of a 30 year loan on a €200,000 flat with nothing down and a 5% interest rate. If it is not already completely obvious, the reason you can still lose money is because of all the interest paid.

Contrary to what you might have heard in the media, a mortgage is not a “forced savings plan”. It is a forced series of cash flows you must make in order to retain your house, but it is not a savings plan. The interest portion of the payments will never come back to you. That money is totally gone. Only the principal portion of the loan can possibly be construed to be savings in some sense of the word. And unfortunately, as you can see from the payment schedule shown above, most of the payment in the early years is interest.

Think about how unappealing the sales pitch sounds when stripped down to the raw math: “Invest €12,884 with us this year! At the end of the year, we guarantee that we well give you back at least €2,951! But wait! It is even better than that! Invest €128,837 with us for 10 years. At the end of the 10 years, we guarantee that we will give you back a whopping €37,316!” The risk becomes obvious: there is the potential for substantial loss.

The Accrual View

As usual, an accrual view of the loan payments provides some good insight. The interest portion of the monthly payment is gone, gone forever. It is clearly an expense that you incur each month for borrowing the money, and your net worth clearly decreases by that amount. On the other hand, the principal portion is a transfer payment. As we have discussed in many of these articles, a transfer payment simply moves money around between your accounts.

So should the principal you paid be considered savings? The answer to that depends on what you find when you look across your entire finances. The act of transferring money (i.e. making your monthly payment) is not in and of itself saving money. However, if you saved €240 during the first month, it does not cease to be savings just because you applied it to your mortgage. Conversely, if you did not save any money that month, you do not magically create €240 in savings by making the payment.

Savings can be generically defined as income minus expenses. Thus, if your income was higher than your expenses last month, you saved money. Where accrual accounting differs from cash accounting is in regards to when something becomes income and when something becomes an expense. On an accrual basis, an expense is recognized when it is incurred, not when it is paid, and income is recognized when it is earned, not when it is received. The previous budgeting articles contain a lot of income and expense examples.

In our opinion, an accrual view provides a much better picture of your household finances. First, strip out all the transfer payments, like the principal portion of your mortgage, credit card principal payments (repayment, but not the interest!), and simply transferring money in and out of accounts. Second, recognize expenses when they are incurred. If you charged €1,000 on your credit card last month, most of that should probably be recognized as an expense immediately, not later when you pay the bill. This gives you an honest picture and keeps you from playing silly mental games like deferring your credit card payment into next month “to save money this month”. Third, ideally you would handle big-ticket depreciation items properly, but if you only do the first two steps, you will still be on the right track.

Someone once asked us if any budgeting software had a “button” you could push to give you an accrual view of your finances instead of a cash view. This is not really the right idea. Any budgeting software or even a simple spreadsheet will automatically give you both a cash and accrual view of your finances if you give it the right data. Your financial data must be broken down into small pieces and classified. In other words, if you only enter the fact that you transferred €1,200 to your credit account on January 20th, then no budgeting software will be able to tell you anything much beyond that. But if you break out the individual purchase transactions and interest expenses, then the accrual view will happen automatically. The key is breaking down the data first, and some software can help with that because it can calculate mortgage payments and download credit card transactions and so forth.

But once the data is broken down and properly classified in the system, both the cash and accrual views will now exist: the cash view is simply the money inflows and outflows relative to the account(s) you are interested in at the moment, and the accrual view is the picture across all accounts. This is why accrual accounting is strongly linked to changes in net worth.

How is a loan amortization schedule calculated?

While we are discussing amortization schedules, let us talk about how they are actually constructed. We see all manner of financial quackery written about amortization schedules, and it appears a lot of misunderstandings and bad decisions follow from not having a true understanding of how this process works.

So let us look closer at the first years in the amortization schedule: The calculations are straightforward. Look at the first year. You owe €200,000. Your interest rate is 5% and you are making a monthly payment. Thus, the interest for the month is simply €200,000 x 0.05 / 12 = €833.33. That is the amount in interest you have to pay that month because you owe €200,000.

Now if you had an interest-only loan, that would in fact be all there is to it. Every month in the loan schedule would be the same. You would pay €833.33 each month for the interest, the loan balance would never go down, and you would still owe €200,000 when the loan was due.

In this case, however, we have a loan that is being paid off over 30 years. This means we need to gradually pay off the principal balance. So looking at the months again, we see that we had to pay €833.33 in interest because we owe €200,000, and we also see that we paid €240.31 in principal. The €240.31 is simply what is left over from the €1,073.64 fixed monthly payment. (€1073.64 – €833.33 = €240.31) For now, do not worry about how we came up with €1,073.64 – that is the only tricky part! So we started with a loan balance of €200,000 and we paid down €240.31, leaving an ending balance of €199,759.69.

Now on to the second month. You will notice that since we paid down a little bit (€240.31) of the principal last month, the interest to pay (€832.33) is now slightly less than the last month. Use the exact same interest formula as before: €199,759.69 x 0.05 / 12 = €832.33. Since the interest is slightly less and the monthly payment is constant, this means the principal payment is slightly increased by that same amount. The interest payment plus the principal payment must always equal the fixed monthly loan payment. This explains why the interest portion goes down slowly over time, while the principal portion goes up slowly by the same amount. This process gets repeated for every month.

As you can see, calculating the numbers requires nothing but basic arithmetic – addition, subtraction, multiplication, and division. Given the first line of the table and enough time to do the calculations, an average 5th grader ought to be able to fill out the rest of the table. If the student was careful, when he or she got to the last line, the ending balance should be zero and the date should be 30 years out.

If you are skilled at creating spreadsheets, you can create a mortgage loan amortization schedule in just a few minutes. You just have to type in the formulas for the first row and then copy/paste to all the other rows. By changing the total monthly payment, you will change the length of the loan – higher payments mean a quicker loan payoff and lower payments mean a slower loan payoff. If you spend a few minutes playing a game of “too high / too low”, you will quickly arrive at a number which is the right value to use for 30 years — that is, one which drives the loan balance to zero in exactly 30 years. That’s where the €1,073.64 monthly payment came from. It is simply the fixed monthly payment that must be used to pay off the loan in the specified time period (30 years in the example).

Now it turns out that mortgage calculators do not actually need to iterate through all the guesses because clever people have figured out ways to calculate these values directly. If you find that sort of thing interesting, you can read more about it in this Wikipedia entry on amortization.

Unlike what you might have heard in the blogosphere, banks do not conspire to concoct special loan schedules to “front-load” the interest or delay the principal payments. The reason the interest payments are higher at first is simply because you owe more money. Once you pay some of the loan back via principal payments, then the loan balance decreases and you pay less interest.

Also, most people want low monthly payments, which means that the length of the loan will be long, which in turn means that the principal payments start out small and hence most of the total monthly payment ends up going to interest at first. Banks might be guilty of many other things, but an amortization schedule is constructed purely based on arithmetic.

A Final Word About Real Estate

Real estate transactions usually involve a large amount of money and are not easily fractionalized. Thus, when individuals purchase a piece of property they usually borrow most of the money. In this respect, the average individual investor who purchases real estate is probably in unfamiliar territory, as individuals do not often borrow money to fund investments.

Every investor must understand that borrowing money sets a very high bar because the rate of the return must first cover the borrowing costs. Simply put, if you borrow substantially all of the money to purchase a property, the property must return as much as the mortgage rate (and other costs) just to break even. This fact leads to a rather sobering conclusion.

The base case for a nonrental, second home as an investment is poor.

Notice, however, the careful wording of the previous sentence.

• Base case. This means the averages are not in your favor. Of course it is possible to eary money. In fact, you can sometimes eary spectacular amounts of money in a few years. Real estate markets are not as efficient as many other markets. But the base case is not very good when you take into account the other following limitations.
• If you can rent out the property to stable tenants at a good price, you can eary money. Keep in mind, however, that you have to cover a lot of costs. It is not as easy as you might think to eary money.
• The example concerned purchasing a second home as an investment. The base case for a principal residence is considerably more favorable. The reason is that you have to live somewhere. Hence, if the cost is favorable compared to renting, then it may still be a good idea.
• Lastly, let us make one thing clear. We never take issue with people who buy a second home because they have always wanted to own a second cabin in the woods or a mansion on the ocean. What other people spend their money on is their business. We just do not think we should label spending money as “investing” in cases where it is not.

A Tale of Two Loans 

Suppose a friend came to you for advice and started the conversation like this:

“I have a great idea. We have been researching mutual funds and we think we have come across real winners. I am convinced it will do really well in the long run. I understand there will be ups and downs, but over time I think it will return 9% annually. The fund only charges 1.38% each year in management fees, and there is a 6% redemption charge as well. I also hear there are some other fees, but I do not think those fees will be too much money.”

“Although I don’t have much money saved up, we are so confident about the fund that we are going to borrow €200,000 and use that to buy shares. The interest rate on the loan is only 10%. So what do you think? Does not it sound like a good idea?”

With a story like that, you probably think your friend is either really naive or really aggressive, and perhaps even a bit crazy, too.

So why do some people think the math changes just because it involves real estate? If you have a property you expect to appreciate 4% per year, and you start with a 5% mortgage, a 1.38% property tax rate, a 6% sales commission, and unknown maintenance costs, it is not really much different from the first example, is it?

Over long periods of time, the appreciation rate of real estate has roughly equaled the wage appreciation rate, which is about inflation plus 1%. This means it is highly likely that the appreciation rate of your property will be less than your mortgage rate. On top of that, the average property tax rate is between 1% – 2%, and every property has substantial maintenance costs as well.

So while real estate can be a good investment, you must understand that the underlying facts are heavily stacked against a nonrental, second home. There are no easy paths to wealth. If you are going to buy a property, be prepared to either live in it, rent it out, or treat it as an expense.